(αρχική φωτό από άρθρο του Gravity and Levity)
Ο Βαγγέλης Δούρος είναι μεταδιδακτορικός ερευνητής δικτύων τηλεπικοινωνιών, χρησιμοποιώντας εφαρμογές οικονομικών και θεωρίας παιγνίων για να τα κατανοήσει καλύτερα. Στον ελεύθερό του χρόνο, ασχολείται (προφανώς) με το μπάσκετ και τον βρίσκετε στο twitter ως @douros. Επίσης είναι αναγνώστης του ιστότοπου για μπάσκετ, Basketballguru.gr.
Μερικά Ερωτήματα
Υπάρχουν περιπτώσεις που η λύση για τη μείωση της κυκλοφοριακής συμφόρησης είναι το κλείσιμο ενός εκ των καλύτερων δρόμων του οδικού δικτύου. Πώς εξηγείται αυτό το παράδοξο φαινόμενο; Τι σχέση μπορεί να έχει με τις απώλειες σημαντικών μονάδων μιας ομάδας μπάσκετ και τη θετική επίπτωση που κάποιες φορές μπορεί να έχουν αυτές οι απώλειες στην αγωνιστική της παρουσία; Τι σχέση έχουν όλα αυτά με το πώς θα μπορούσε να αποφασίσει ένας προπονητής για το ποιος θα τρέξει ένα σύστημα στο τέλος ενός κρίσιμου αγώνα;… Θα έπρεπε να αποκτήσει ο ΠΑΟ ένα point guard με δημιουργικές ικανότητες και ένα παίκτη στο «5», όπως υποστηρίζω εδώ και πολύ καιρό;
Κατόπιν «δημόσιας» πρόσκλησης του editor-in-chief της φιλόξενης αυτής σελίδας, θα προσπαθήσουμε να απαντήσουμε στα περισσότερα από τα παραπάνω ερωτήματα (δε θα μας απασχολήσει το τελευταίο).
Ένα Πρόσφατο Παράδειγμα
Ο (Άγιος) Γεώργιος Πρίντεζης λίγο πριν ξεκινήσει ο αγώνας με την Μπάμπεργκ αισθάνθηκε ενοχλήσεις στη μέση και δεν κατάφερε να αγωνιστεί. Η απώλειά του προκάλεσε εύλογη ανησυχία στους φιλάθλους της ομάδας, δεδομένου ότι:
· Το πρόβλημα προέκυψε τελευταία στιγμή.
· Ο Πρίντεζης είναι από τα καλύτερα 4αρια της Ευρώπης.
· Το μόνο άλλο κλασσικό 4αρι του ΟΣΦΠ τα 2 τελευταία χρόνια είναι ο Αγραβάνης, συνεπώς η θέση 4 πρέπει να καλύπτεται συχνά με παίκτες που δεν είναι κλασσικά 4άρια και αυτό δεν αρέσει πάντα στους φιλάθλους της ομάδας.
· Η Μπάμπεργκ είναι ο κακός δαίμονας του ΟΣΦΠ, κάτι αντίστοιχο με τη Λιμόζ της δεκαετίας του 1990 (αλλά η Μπάμπεργκ παίζει πολύ πιο ελκυστικό μπάσκετ, έργο Τρινκιέρι γαρ).
Ο ΟΣΦΠ όμως κέρδισε και η απουσία του Πρίντεζη δεν πολυφάνηκε. Πώς κατάφερε ο ΟΣΦΠ να καλύψει το κενό του υπαρχηγού του και να φτάσει σε άλλο ένα νικηφόρο αποτέλεσμα; Γενικότερα, πώς καταφέρνει μια ομάδα να καλύψει μια τέτοια απουσία;
Μια Αληθοφανής Εξήγηση
Η κλασσική ερμηνεία εδράζεται στον τομέα της ψυχολογίας: Η απουσία ενός κομβικού παίκτη συσπειρώνει τους υπόλοιπους, οι οποίοι αγωνίζονται με μεγαλύτερο πάθος και δίνουν τον καλύτερο εαυτό τους για να παίξουν και για τον απόντα συμπαίκτη τους. Μήπως όμως αυτή η αληθοφανής ερμηνεία δεν είναι επαρκής/ενδεδειγμένη; Μήπως συντρέχουν άλλοι μετρήσιμοι λόγοι ώστε η απώλεια ενός πολύ καλού παίκτη (όχι του Πρίντεζη εν προκειμένω) να λειτουργεί ευεργετικά για την ομάδα;
Less is More: Λιγότεροι Δρόμοι, Λιγότερη Κίνηση
Βρισκόμαστε στο 1968 και ο καθηγητής μαθηματικών Dietrich Braess δημοσιεύει την εργασία “Üζber ein Paradoxon aus der Verkehrsplanung” (αν δε γνωρίζετε γερμανικά, η εργασία επαναδημοσιεύτηκε στα αγγλικά αρκετά χρόνια μετά και είναι προσβάσιμη εδώ) που σημαίνει σε ελεύθερη απόδοση “Ένα παράδοξο στη σχεδίαση οδικών δικτύων” και επιχειρηματολογεί για το εξής: Η προσθήκη ενός αυτοκινητοδρόμου μπορεί να οδηγήσει σε αύξηση της κυκλοφοριακής συμφόρησης στο οδικό δίκτυο.
Πάμε να δούμε με τη βοήθεια της Εικόνας 1 πώς μπορεί να συμβεί κάτι τέτοιο (η αρχική έκδοσή του παραδείγματος βρίσκεται εδώ).
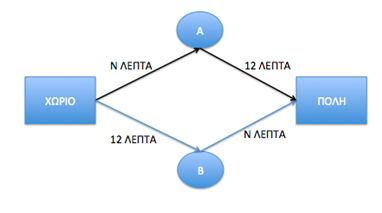
Εικόνα 1: Ένα απλό οδικό δίκτυο. Σε κάποιες διαδρομές, ο χρόνος της διαδρομής είναι συνάρτηση του πλήθους των αυτοκινητών (Ν).
Ν=10 αυτοκίνητα ξεκινούν την ίδια ώρα από το χωριό για να πάνε στην πόλη. Υπάρχουν δυο εναλλακτικές διαδρομές. Η πρώτη διαδρομή έχει ως εξής:
• Από το χωριό στο σημείο Α μέσω ενός στενού δρόμου σε χρόνο που εξαρτάται από το πλήθος των αυτοκινήτων που θα το χρησιμοποιήσουν. Θα απαιτηθούν Ν λεπτά αν χρησιμοποιήσουν το δρόμο Ν αυτοκίνητα.
• Στη συνέχεια, υπάρχει δρόμος ταχείας κυκλοφορίας από το σημείο Α στην πόλη σε σταθερό χρόνο 12 λεπτών.
Η δευτερη διαδρομή αποτελείται από αντίστοιχους δρόμους με ανάποδη σειρά: Αρχικά, το δρόμο ταχείας κυκλοφορίας μέχρι το σημείο Β διάρκειας 12 λεπτών και στη συνέχεια απαιτούνται Ν λεπτά, ανάλογα με το πλήθος Ν των αυτοκινήτων που θα χρησιμοποιήσουν το δρόμο.
Η διάρκεια κάθε διαδρομής είναι 12+Ν λεπτά, γεγονός που σημαίνει ότι ένα αυτοκίνητο μπορεί να φτάσει στην πόλη σε 13 λεπτά στην καλύτερη περίπτωση (αν μόνο αυτό επιλέξει το στενό δρόμο) και σε 22 λεπτά στη χειρότερη περίπτωση (αν και τα 10 αυτοκίνητα επιλέξουν τον ίδιο στενό δρόμο).
Αυτό που αναμένουμε ότι θα συμβεί είναι ότι 5 αυτοκίνητα θα επιλέξουν την πρώτη διαδρομή και 5 αυτοκίνητα τη δέυτερη διαδρομή, συνεπώς ο συνολικός χρόνος διαδρομής για κάθε αυτοκίνητο θα είναι 17 λεπτά. Ο λόγος είναι ότι αυτή είναι η μοναδική περίπτωση όπου κανένα αυτοκίνητο δε θα είχε κίνητρο να αλλάξει διαδρομή (γιατί αν άλλαζε διαδρομή, τότε θα έκανε περισσότερο χρόνο). Αυτή η κατάσταση αντιστοιχεί στο μοναδικό σημείο ισορροπίας του συστήματος.
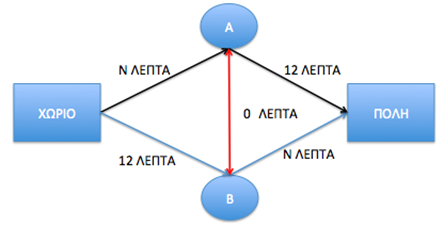
Εικόνα 2: Το νέο οδικό δίκτυο μετά την προσθήκη ενός δρόμου υπερταχείας κυκλοφορίας από το σημείο Α στο σημείο Β.
Το χωριό σε συνεργασία με την πόλη αποφασίζει να κατασκευάσει ένα δρόμο υπερταχείας κυκλοφορίας, συνδέοντας τα σημεία Α και Β σε πολύ μικρό χρόνο (πρακτικά μηδέν). Η νέα μορφή του οδικού δικτύου αποτυπώνεται στην Εικόνα 2. Με αυτό τον τρόπο, οι αρχές της πόλης και του χωριού αναμένουν ότι ο χρόνος μετάβασης θα μειωθεί δραστικά. Τα πράγματα όμως δεν είναι όπως φαίνονται. Ένα αυτοκίνητο μπορεί να φτάσει στο σημείο Α σε Ν=10 το πολύ λεπτά που είναι προτιμότερο από τα 12 λεπτά για να πάει από το χωριό στο σημείο Β. Από το σημείο Α έχει πλέον 2 επιλογές: Να πάει κατευθείαν στην πόλη σε 12 λεπτά ή να χρησιμοποιήσει τον καινούργιο δρόμο φτάνοντας στο σημείο Β σε χρόνο μηδέν και από εκεί να φτάσει στην πόλη σε Ν=10 το πολύ λεπτά. Όλα τα αυτοκίνητα έχουν πλέον κίνητρο να επιλέξουν τη διαδρομή Χωριό--->Α--->Β--->Πόλη, συνεπώς ο χρόνος μετακίνησης είναι πλέον 10+0+10=20 λεπτά, δηλ. 3 λεπτά παραπάνω από την περίπτωση που δεν είχε προστεθεί ο καινούργιος δρόμος υπερταχείας κυκλοφορίας!
To παράδοξο αυτό, το οποίο ονομάστηκε Braess Paradox προς τιμήν του καθηγητή, δεν είναι μια θεωρητική παρατήρηση άνευ πρακτικού αντικρίσματος. Παρατηρήθηκε στην πράξη σε διάφορες πόλεις (π.χ., Στουτγκάρδη, Νέα Υόρκη, Σεούλ) τα τελευταία χρόνια---σχετικές αναφορές υπάρχουν στη σχετική σελίδα της wikipedia. Η κυκλοφορία των αυτοκινήτων στις πόλεις αυτές βελτιώθηκε όταν ένας μεγάλος δρόμος έκλεινε.
Επιθετικά Συστήματα στο Μπάσκετ vs. Επιλογές Δρόμων σε Οδικά Δίκτυα
Ωραία όλα αυτά, αλλά τι σχέση έχουν με το μπάσκετ και την απώλεια ενός πολύ σημαντικού παίκτη;
Ας ασχοληθούμε αρχικά με το 1ο σκέλος του ερωτήματος. Το 2011, ο Brian Skinner, μεταδιδακτορικός ερευνητής στο MIT, δημοσίευσε την εργασία “The price of anarchy in basketball”, την οποία μπορείτε να βρείτε εδώ. Στην εργασία αυτή παραλλήλισε το χωριό με το σημείο που αρχίζει η επίθεση μιας ομάδας, τις εναλλακτικές διαδρομές με τα εναλλακτικά συστήματα και την πόλη με το αντίπαλο καλάθι.
Το απλουστευμένο (αλλά όχι απλοϊκό) αυτό μοντέλο μάς επιτρέπει να εξετάσουμε υπό ένα διαφορετικό πρίσμα τις επιλογές μιας επίθεσης στο μπάσκετ.
Ας συζητήσουμε το σύστημα επίθεσης (play) που φαίνεται στην Εικόνα 3, ελαφρά τροποποιημένο από την παραπάνω αναφερόμενη εργασία.
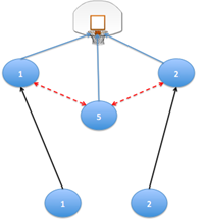
Εικόνα 3: Ένα «ειδικό» play. Με μαύρο βελάκι, η κίνηση των παικτών, με κόκκινο βελάκι οι πιθανές πάσες, με μπλε βελάκι το σουτ.
Στο play συμμετέχουν οι 3 καλύτεροι παίκτες της ομάδας: o point guard (1), o shooting guard (2) και ο center (5).
Το play ξεκινά είτε από το (1) είτε από το (2). Όποιος πάρει την μπάλα κάνει το drive όπως φαίνεται στα μαύρα βελάκια και εκεί έχει 2 επιλογές: Ή να σουτάρει ή να δώσει πάσα στο (5). Αν δώσει πάσα, το (5) έχει δύο επιλογές: Ή να σουτάρει ή να δώσει πάσα στον παίκτη που έχει κόψει στην αδύνατη πλευρά---αν π.χ. έτρεξε το play το (1), ο (5) μπορεί είτε να σουτάρει είτε να δώσει πάσα στο (2) και αυτός είναι που θα σουτάρει.
Κωνσταντινούπολη, Μάης 2017, τελικός Ευρωλίγκας, 78-77 και απομένουν 7 δευτερόλεπτα. Ο προπονητής της ομάδας που χάνει, καλεί το τελευταίο του time out και αποφασίζει να εφαρμόσει το παραπάνω ειδικό play .
Τα ερωτήματα είναι τα εξής:
1. Θα ξεκινήσει το play ο (1) ή ο (2);
2. Ο παίκτης που θα κανει το drive θα σουτάρει ή θα πασάρει στο (5);
3. Αν πασάρει στο (5), ο (5) θα σουτάρει ή θα δώσει πάσα στον παίκτη που έχει κόψει στην αδύνατη πλευρά για να σουτάρει αυτός;
Πάμε να δούμε πώς θα μπορούσε να σκεφτεί ο προπονητής, υποθέτωντας ότι έχει στη διάθεσή του τα δεδομένα του Πίνακα 1.
• Αν ξεκινήσει το drive ο (1), η πιθανότητα να φτάσει στο σημείο που του ζήτησε ο προπονητής (εκεί που δείχνει το μαύρο βελάκι) είναι 0.5. Θυμίζουμε ότι η πιθανότητα είνει ένας αριθμός από το 0 (που σημαίνει ότι το γεγονός δε συμβαίνει ποτέ), μέχρι το 1 (που σημαίνει ότι το γεγονός συμβαίνει πάντα).
• Αν ξεκινήσει το drive ο (2), η πιθανότητα να φτάσει στο σημείο που του ζήτησε ο προπονητής δίνεται από τον τύπο 1-0.5x. Το x είναι ένας (κανονικοποιημένος) αριθμός από το 0 μέχρι το 1 που εκφράζει τη σχετική συχνότητα του γεγονότος να ξεκινήσει το play από το (2). Αν το x είναι 0, το play δεν αρχίζει ποτέ από το (2), αν το x είναι 1 το play αρχίζει πάντα από το (2). Παρατηρούμε ότι όσο πιο συχνά εφαρμόζεται το play με αφετηρία το (2), δηλ. όσο πιο μεγάλο είναι το x, τόσο μικραίνει η πιθανότητα επιτυχίας. Η αντίπαλη άμυνα προσαρμόζεται στο play, λογικό δεν είναι;
| ΠΙΘΑΝΟΤΗΤΑ ΝΑ ΦΤΑΣΕΙ Ο ΠΑΙΚΤΗΣ ΠΟΥ ΞΕΚΙΝΑ ΤΟ DRIVE ΣΤΟ ΣΗΜΕΙΟ ΠΟΥ ΔΕΙΧΝΕΙ ΤΟ ΜΑΥΡΟ ΒΕΛΑΚΙ | ΠΙΘΑΝΟΤΗΤΑ ΕΥΣΤΟΧΙΑΣ (ΜΠΛΕ ΒΕΛΑΚΙ) | |
| ΠΑΙΚΤΗΣ (1) | 0.5 | 1-0.5z |
| ΠΑΙΚΤΗΣ (2) | 1-0.5x | 0.5 |
| ΠΑΙΚΤΗΣ (5) | - | 0.75-0.25y |
Παρατηρούμε επίσης ότι το χειρότερο σενάριο για την περίπτωση που ξεκινήσει το drive ο (2) είναι να έχει πιθανότητα επιτυχίας 1-0.5 x 1=0.5, δηλ. όση η πιθανότητα επιτυχίας αν ξεκινήσει το drive από το (1).
Με βάση τα παραπάνω, μπορούμε να απαντήσουμε το ερώτημα «Θα ξεκινήσει το play ο (1) ή ο (2);». Αναμένουμε ότι ο προπονητής στο time out θα πει: «Το drive θα γίνει από το (2)».
Πάνε να απαντήσουμε στο 2ο ερώτημα: «Ο παίκτης που θα κανει το drive θα σουτάρει ή θα πασάρει στο (5);». Από τον πίνακα 1, παρατηρούμε ότι ο (2) σουτάρει με πιθανότητα επιτυχίας 0.5 ενώ ο (5) με πιθανότητα επιτυχίας 0.75-0.25y, όπου y ένας (κανονικοποιημένος) αριθμός από το 0 μέχρι το 1 που εκφράζει τη σχετική συχνότητα του γεγονότος να πάρει το σουτ το (5). Αν ο (5) σουτάρει συχνά, η αντίπαλη άμυνα προσαρμόζεται, συνεπώς ο παίκτης ευστοχεί σπανιότερα, λογικό δεν είναι;
Παρατηρούμε ότι το η πιθανότητα επιτυχίας του (5) είναι στη χειρότερη περίπτωση 0.75-0.25 x 1=0.5.
Με βάση τα παραπάνω, αναμένουμε ότι ο προπονητής στο time out θα πει: «Μετά το drive του (2), ο (2) πασάρει στο (5)».
Πάμε λοιπόν και στο 3ο ερώτημα: “Αν πασάρει στο (5), ο (5) θα σουτάρει ή θα δώσει πάσα στον παίκτη που έχει κόψει στην αδύνατη πλευρά για να σουτάρει αυτός;».
Εντωμεταξύ, ο (1) έχει κόψει στο low post και από τη θέση αυτή έχει πιθανότητα επιτυχίας 1-0.5z, όπου z (κατά τα γνωστά) ένας (κανονικοποιημένος) αριθμός από το 0 μέχρι το 1 που εκφράζει τη σχετική συχνότητα του γεγονότος να πάρει το σουτ ο (1).
Παρατηρούμε ότι η πιθανότητα επιτυχίας του (1) είναι στη χειρότερη περίπτωση 1-0.5 x 1=0.5. Τόσο όμως είναι και για το (5).
Τι θα πρέπει να επιλέξει ο προπονητής; Η απάντηση θα μπορούσε να είναι ότι θα πρέπει να μπερδέψει την αντίπαλη άμυνα και να δώσει με διαφορετική (σχετική) συχνότητα την μπάλα στο (1) και στο (5). Οι παίκτες θα είναι εξίσου αποτελεσματικοί όταν η πιθανότητα επιτυχίας του σουτ είναι ίδια, ανεξάρτητα από το ποιος θα σουτάρει. Αυτό σημαίνει ότι θα πρέπει 0.75-0.25y=1-0.5z και επειδή ή θα σουτάρει ο (5) ή ο (1), θα πρέπει επίσης y+z=1. Λύνοντας το παραπάνω σύστημα εξισώσεων (που απαιτείς γνώσεις μαθηματικών Γ΄Γυμνασίου), βρίσκουμε ότι ο προπονητής πρέπει να αποφασίσει να σουτάρει ο (1) με σχετική συχνότητα z=2/3 και ο (5) με σχετική συχνότητα y=1/3.
Ποια είναι τελικά η πιθανότητα επιτυχίας του play; Κάθε παίκτης θα ευστοχήσει με πιθανότητα 1-0.5 x 2/3=0.75-0.25 x 1/3=2/3. Τέλος, επειδή όπως απαντήσαμε στο ερώτημα 1, το play θα ξεκινήσει πάντα από το (2), αυτό σημαίνει ότι η πιθανότητα του (2) να φτάσει στη θέση που δείχνει το βελάκι θα είναι 1-0.5 x 1=0.5. Οπότε, τελικά, το play θα είναι πετυχημένο με πιθανότητα 0.5 x 2/3=1/3=0.33.
To παράδοξο του Braess στο μπάσκετ
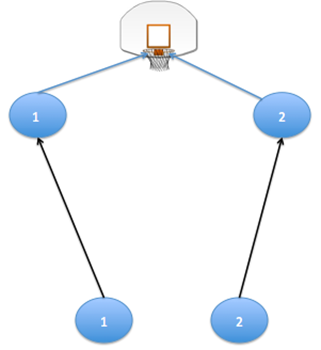
Εικόνα 5: Το ίδιο play χωρίς την παρουσία του (5).
Πάμε να δούμε το ίδιο play στην περίπτωση που ο πολύ καλός παίκτης στο (5) έχει τραυματιστεί/αποβληθεί κ.λπ. και ο αντικαταστάτης του δεν εμπλέκεται σε αυτό. Σε αυτή την περίπτωση, όπως φαίνεται στην εικόνα 5, είτε ο (1) είτε ο (2) θα τρέξει όλη την επίθεση μόνος του. Διατηρώντας τα δεδομένα του Πίνακα 1 για τις πιθανότητες επιτυχίας τόσο του drive όσο και του σουτ από το low post, έχουμε:
• Αν ο προπονητής επιλέξει το (1), ο παίκτης θα σκοράρει με πιθανότητα 0.5(1-0.5z).
• Αν ο προπονητής επιλέξει το (2), ο παίκτης θα σκοράρει με πιθανότητα (1-0.5x)0.5.
Αναμένοντας ότι ο προπονητής θα προσπαθήσει να μπερδέψει την αντίπαλη άμυνα και λαμβάνοντας επιπλέον υπόψιν ότι x+z=1, καταλήγουμε ότι x=z=0.5. Αντικαθιστώντας τα x και z με το 0.5, βρίσκουμε ότι πιθανότητα επιτυχίας του play είναι πλέον 0.375.
Τι σημαίνει αυτό; Η ομάδα έχασε το βασικό της “5” που έχει το 2ο καλύτερο ποσοστό ευστοχίας στο συγκεκριμένο play, αλλά παρόλα αυτό το play έχει μεγαλύτερη πιθανότητα πλέον να είναι επιτυχημένο (0.375 έναντι 0.33). Παράδοξο μεν, λογικό δε.
Αντί Επιλόγου
Παρεμπιπτόντως, αν ο προπονητής ενδιαφέρεται να εκτελέσει το συγκεκριμένο play 100 φορές, μήπως θα είχε νόημα να ξεκινήσει κάποιες επιθέσεις και ο (1); Γενικότερα, μήπως είναι αποδοτικότερο κάποιες φορές ο καλύτερος σουτέρ της ομάδας να παίρνει λίγες/λιγότερες προσπάθειες; Υπάρχουν ενδείξεις ότι το Braess paradox έχει συμβεί σε κάποιες ομάδες; Ίσως τα συζητήσουμε κάποια άλλη φορά.